Natural numbers are a fundamental concept in mathematics. They are used every day for counting and ordering. This article will explain what they are, their properties, and their role in the number system.
What Are Natural Numbers?
Natural numbers are positive integers starting from 1 and going on forever. They do not include zero, fractions, decimals, or negative numbers.
Definition
They are defined as:
- Positive integers
- Starting from 1
- Continuing infinitely
Set Notation:
It is written as N={1,2,3,4,5,…}N = \{1, 2, 3, 4, 5, \ldots\}N={1,2,3,4,5,…}
Examples
Here are a few examples
- 1
- 2
- 3
- 10
- 100
The Smallest Natural Number
The smallest natural number is 1. It always starts from 1.
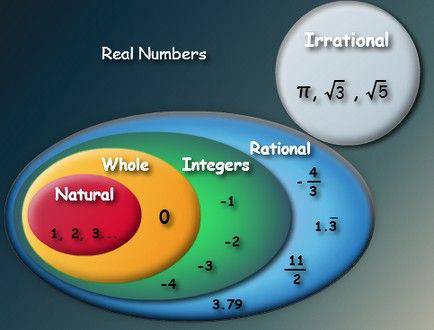
Natural Numbers vs. Whole Numbers
Natural numbers and whole numbers are closely related but differ slightly.
Natural Numbers
- Set Notation: N={1,2,3,4,…}N = \{1, 2, 3, 4, \ldots\}N={1,2,3,4,…}
- Smallest Number: 1
- Examples: 1, 2, 3, 4, 100
Whole Numbers
- Set Notation: W={0,1,2,3,4,…}W = \{0, 1, 2, 3, 4, \ldots\}W={0,1,2,3,4,…}
- Smallest Number: 0
- Examples: 0, 1, 2, 3, 100
Key Difference: Whole numbers include zero, while natural numbers do not.
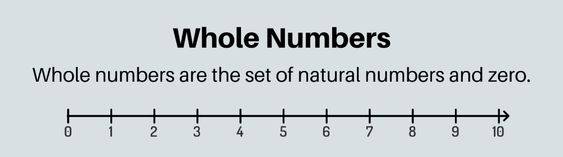
Representing Natural Numbers
They can be shown on a number line.
Number Line
On a number line:
- They are the positive integers to the right of zero.
- They continue infinitely.
Properties of Natural Numbers
They have several important properties:
Closure Property
- Addition: The sum of two natural numbers is always a natural number.
Example: 2+3=52 + 3 = 52+3=5 - Multiplication: The product of two natural numbers is always a natural number.
Example: 4×5=204 \times 5 = 204×5=20 - Not Applicable: Subtraction and division may not always result in a natural number.
Associative Property
- Addition: Changing the grouping of numbers does not change the result.
Example: (1+2)+3=1+(2+3)(1 + 2) + 3 = 1 + (2 + 3)(1+2)+3=1+(2+3) - Multiplication: Changing the grouping does not change the result.
Example: (2×3)×4=2×(3×4)(2 \times 3) \times 4 = 2 \times (3 \times 4)(2×3)×4=2×(3×4)
Commutative Property
- Addition: Changing the order of numbers does not change the result.
Example: 3+4=4+33 + 4 = 4 + 33+4=4+3 - Multiplication: Changing the order does not change the result.
Example: 2×5=5×22 \times 5 = 5 \times 22×5=5×2
Distributive Property
- Over Addition: Multiplication distributes over addition.
Example: 2×(3+4)=(2×3)+(2×4)2 \times (3 + 4) = (2 \times 3) + (2 \times 4)2×(3+4)=(2×3)+(2×4) - Over Subtraction: Multiplication distributes over subtraction.
Example: 2×(5−3)=(2×5)−(2×3)2 \times (5 – 3) = (2 \times 5) – (2 \times 3)2×(5−3)=(2×5)−(2×3)
Odd and Even Natural Numbers
It can be classified as odd or even.
Odd Natural Numbers
Odd natural numbers are those not divisible by 2:
- Examples: 1, 3, 5, 7
Even Natural Numbers
Even natural numbers are divisible by 2:
- Examples: 2, 4, 6, 8
Operations with Natural Numbers
Natural numbers can be used in various operations.
Addition
Adding two natural numbers always results in a natural number.
Example: 7+8=157 + 8 = 157+8=15
Subtraction
Subtracting one natural number from another does not always result in a natural number.
Example: 7−3=47 – 3 = 47−3=4 (which is a natural number)
Example: 5−7=−25 – 7 = -25−7=−2 (which is not a natural number)
Multiplication
Multiplying two natural numbers always results in a natural number.
Example: 6×4=246 \times 4 = 246×4=24
Division
Dividing one natural number by another may not always result in a natural number.
Example: 8÷4=28 \div 4 = 28÷4=2 (which is a natural number)
Example: 7÷2=3.57 \div 2 = 3.57÷2=3.5 (which is not a natural number)
Frequently Asked Questions
Are Natural Numbers and Integers the Same?
Answer: No, they are not the same. Natural numbers are positive integers starting from 1, while integers include all positive and negative whole numbers, as well as zero. For example, {-3, -2, -1, 0, 1, 2, 3, \ldots} are integers, but only {1, 2, 3, \ldots} are natural numbers.
Are Natural Numbers Rational Numbers?
Answer: Yes, natural numbers are a subset of rational numbers. Rational numbers are numbers that can be expressed as a fraction pq\frac{p}{q}qp where ppp and qqq are integers and q≠0q \neq 0q=0. Natural numbers can be expressed as n1\frac{n}{1}1n, where nnn is a natural number.
Can Natural Numbers Be Negative?
Answer: No, natural numbers cannot be negative. They are only positive integers starting from 1. Negative numbers are not included in the set of natural numbers.
Is Zero a Natural Number?
Answer: zero is not a natural number. Natural numbers start from 1 and do not include zero. However, zero is included in the set of whole numbers.
What Are the Properties of Natural Numbers?
Answer: Natural numbers have several important properties:
- Closure Property: The sum or product of two natural numbers is always a natural number.
- Associative Property: The grouping of numbers does not affect the result of addition or multiplication.
- Commutative Property: The order of numbers does not affect the result of addition or multiplication.
- Distributive Property: Multiplication distributes over addition and subtraction.
What Is the Difference Between Natural Numbers and Rational Numbers?
Answer: Natural numbers are positive integers starting from 1. Rational numbers include natural numbers and any number that can be expressed as a fraction pq\frac{p}{q}qp, where ppp and qqq are integers and q≠0q \neq 0q=0. This means all natural numbers are rational numbers, but not all rational numbers are natural numbers.
What Is the Sum of the First 100 Natural Numbers?
Answer: To find the sum of the first 100 natural numbers, use the formula for the sum of an arithmetic series:
Sn=n(n+1)2S_n = \frac{n(n + 1)}{2}Sn=2n(n+1)
where nnn is the number of terms. For the first 100 numbers:
S100=100×1012=5050S_{100} = \frac{100 \times 101}{2} = 5050S100=2100×101=5050
Can natural numbers be decimals?
Answer: No, natural numbers cannot be decimals. They are strictly positive integers. Decimals and fractions are not included in the set of natural numbers.
Are all positive Integers natural numbers?
Answer: All positive integers starting from 1 are natural numbers. Negative integers and zero are not included.